My research interests
The sparkle of a rare gemstone is evidence of its perfect crystalline order. Imperfection is not always a disadvantage, though. When present in specific configurations, defects like grain boundaries, can impart added mechanical strength. They can also modify other characteristic properties like thermal conductance. Polycrystalline diamond is an example of this. These are observations and inferences drawn from measurable material properties like elastic moduli, yield point or specific heat of solids. All around us, solids undergoing plastic deformation or exhibiting structural transformation, constantly change states and their material properties. Phenomenological continuum level descriptions, based on a few independent thermodynamic variables, aim to derive constitutive relations like the relation connecting stress and strain in a mechanical deformation experiment. While they provide a qualitative understanding of the static properties or the kinetics of transformations, they often lack any microscopic basis. Observable macroscopic properties obtained at well-defined temperature, pressure etc. emerge from a huge number of microscopic events occurring at several orders of magnitude smaller spatio-temporal scales. My research focuses on understanding the fundamental principles governing such properties or processes. I use a wide array of tools available in the equilibrium and non-equilibrium statistical mechanics toolkit. With recent advances in soft condensed materials, our fundamental microscopic theories, besides having technological implications in manipulating material properties, also offer exciting avenues not limited to the core fields of thermodynamics and statistical mechanics.
"More is different", according to P. W. Anderson. My research strives to discover the difference and rationalise it.
Projects
How to derive elasticity theory when a crystal is not ideal ?
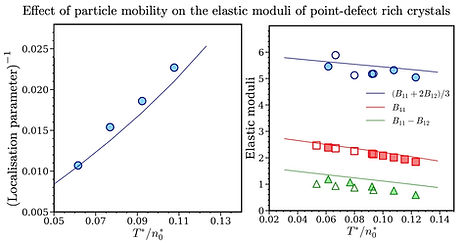
Continuum elasticity theory, widely used to describe the reversible mechanical response in solids, cannot be derived from a first principle microscopic description as soon as defects are introduced in a crystalline solid. The crystalline phase at a finite temperature has a non-zero concentration of vacancies and interstitials. These local-defects influence the reversible mechanical response as well as irreversible transport processes. Starting from the classical many-body Hamiltonian, using Mori-Zwanzig projection formalism, we derive[1] the laws of continuum mechanics governing the elastic response, defect diffusion, and heat transport in non-ideal crystals. The theory finds partial validation[2] through the successful prediction of the isothermal elastic properties of cluster-crystal phases known to mimic DNA-based dendritic nanostructures. The formulation prescribes ways to measure these quantities in atomistic simulations and particle tracking colloidal experiments.
[1]Elasticity in crystals with high density of local defects : insights from ultra-soft colloids
Saswati Ganguly*, GP Shrivastav, S-C Lin, J Häring, R Haussmann, G Kahl, M Oettel and Matthias Fuchs (* indicates communicating author)
The Journal of Chemical Physics 156, 064501 (2022)
[2]Continuum mechanics for the elastic properties of crystals: Microscopic approach based on projection-operator formalism
Florian Miserez, Saswati Ganguly*, Rudolf Haussmann and Matthias Fuchs
Physical Review E 106, 054125 (2022)
Accurate measurement of entropy of interfaces in crystals,
What are the difficulties?
Despite compelling arguments favouring the thermodynamic stability of single crystals, they are exceedingly rare in nature. The mechanical response of crystalline materials is governed by the microstructural events in polycrystals, with their temperature-sensitive grain boundary structures. Entropy is the key to understanding the relative stabilities and the structural transformations of these interfaces at atomic length scales. Measurement of entropy, accurately enough to capture temperature-induced transformations in grain boundary microstructures, proves to be quite non-trivial. We present[3] a thermodynamic integration scheme (involving Molecular Dynamics simulations) that successfully circumvents the conceptual challenges of computing free energy or entropy of solid-solid interfaces like grain boundaries at arbitrary temperatures.
[3]The free energy of grain boundaries from atomistic computer simulation
Saswati Ganguly, Jürgen Horbach

How to use crystal symmetries to obtain insights into grain boundary microstructures?
Do thermodynamically stable rigid solids exist?
Crystalline solids, when subjected to deformation at a constant rate, exhibit a sudden stress drop at the yield-point. The systematic decrease in the yield-point with the lowering of the shear rate presents a conundrum regarding the existence of thermodynamically stable rigid solids. We explain[4] this shear-rate-dependent onset of plasticity in rigid solids in terms of an underlying first-order phase transition between a uniformly stressed crystal to a stress-relaxed ordered state. This perspective implies that even an infinitesimal strain can render a crystalline solid metastable, and the first passage time associated with the decay of the metastable state dictates the yield point of the crystal at a given shear rate. This unique way of interpreting the yielding of ordered solids relies on advanced sampling techniques like successive umbrella sampling Monte Carlo and an extensively derived general spatial projection framework [5, 6] to segregate and quantify displacement fields at microscopic length scales.

[4]On the existence of thermodynamically stable rigid solids
P Nath#, Saswati Ganguly#, Jürgen Horbach, P Sollich, S Karmakar, Surajit Sengupta (# indicates equal first author)
Proceedings of the National Academy of Sciences 115 (19), E4322-E4329, (2018)
[5]Nonaffine displacements in crystalline solids in the harmonic limit
Saswati Ganguly, Surajit Sengupta, P Sollich, M Rao
Physical Review E, 87 (4), 042801, (2013)
A figure from this paper got selected for PRE Kaleidoscope (April 2013)
[6]Statistics of non-affine defect precursors: tailoring defect densities in colloidal crystals using external fields
Saswati Ganguly*, Surajit Sengupta, P Sollich
Soft Matter, 11 (22), 4517, (2015)
Statistical thermodynamics of elastic and plastic response in crystals:
Affine and non-affine displacement perspectives
A macroscopic strain on any ordered structure (like crystalline solids) translates into particle-level uniform stresses or irreversible particle rearrangements. There are observable thermodynamic parameters dictating the measurable responses manifesting as elastic or plastic deformations. However, interpreting them in terms of the laws of statistical mechanics, governing the events at particle-length-scales, proves to be the real challenge. We present[5] a theoretical framework to disentangle (a)particle displacements associated with uniform stress and (b)particle rearrangements leading to a plastic response. Besides recovering Hooke's law[5,6,9] and explicit connections to concepts of topological defect precursors[6,7,8], this general framing of particle displacements finds wide-ranging applications in studies of martensitic transitions, inducing stable structure formation in colloids, understanding pleating mechanisms in membranes, interpreting ligand binding mechanisms in proteins and hopefully many more in future.
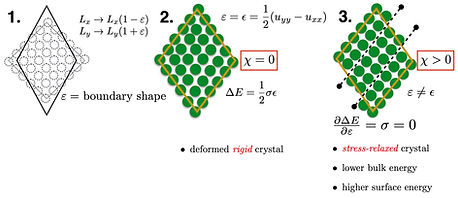
An ordered structure (1) can respond to macroscopic shear strains in two fundamentally distinct ways depicted in (2) and (3). One is affine, the other one is non-affine.
[7]Non-affine fluctuations and the statistics of defect precursors in the planar honeycomb lattice
Amartya Mitra, Saswati Ganguly, Surajit Sengupta, Peter Sollich,
Journal of Statistical Mechanics: Theory and Experiment, 2015 (6), P06025, (2015)
[8]Pre-Yield Non-Affine Fluctuations and A Hidden Critical Point in Strained Crystals
T Das, Saswati Ganguly, Surajit Sengupta, M Rao
Scientific Reports 5, 10644, (2015)
[9]Excess vibrational modes of a crystal in an external non-affine field
Saswati Ganguly, Surajit Sengupta
Insights derived from analogies between pleating of membranes and yielding of a crystalline solid
Folding or pleating of two-dimensional elastic manifolds and landscapes of complex shapes fabricated from them have recently emerged as a viable technological paradigm, applicable over a large range of length scales, from microns to nanometers. A number of these innovative ideas are equally applicable for atomic crystals or for larger assemblies involving functionalized colloidal particles joined together using polymer tethers or micron-sized lipid droplets. Microscopic insights into the underlying thermodynamics and kinetics of these local shape changes can render precise control over local structural properties. Some of our recent studies[10,11] reveal surprising analogies between the principles governing (a)the dynamics of pleating or wrinkle formation in membranes and (b) the shear-rate-dependent onset of plastic deformation in crystalline solids. Identical theoretical and simulation machinery, used in exploring these problems from a statistical mechanics perspective, yields interesting new insights.

[10]Plastic deformation of a permanently bonded network: stress relaxation by microscopic pleats
Saswati Ganguly*, D Das, J Horbach, P Sollich, S Karmakar, Surajit Sengupta
The Journal of Chemical Physics 149, 184503 (2018)
[11]Equilibrium and dynamic pleating of a crystalline bonded network
Saswati Ganguly, P Nath, Jürgen Horbach, P Sollich, S Karmakar, Surajit Sengupta
Intermediate (I) and final (II) stages of system spanning pleats in an elastic membrane, produced by displacing vertices of a regular triangular network of bonds.
Soft condensed matter experiments: Our theories find application and validation
With recent advances in the fields of soft condensed materials, fundamental microscopic theories within the premise of statistical mechanics
have found new grounds to interpret and new avenues of validation. Similar to martensitic structural transition in metals or alloys, colloidal crystals can be induced to undergo structural transition. But unlike metallic solids, single particle trajectories in colloidal crystals can be tracked with high spatio-temporal precision. We propose[12] a way to stabilise colloidal particles in finite translationally invariant lattices without the use of static templates. Conceptual perception and analysis of particle displacements, similar to [12] and initially proposed in references[5,6], were also used in studying[13,14] the crystal-to-crystal (martensitic or diffusion mediated) structural transformation in micron-scale ionic microgel colloids.
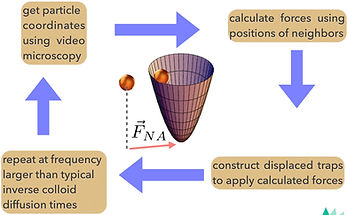
Dynamic template to stabilise colloidal crystals of arbitrary symmetries
[12]Translationally invariant colloidal crystal templates
Pankaj Popli, Saswati Ganguly, Surajit Sengupta
Soft Matter 14 (1), 104, (2018)
[13]Contrasting the dynamics of elastic and non-elastic deformations across an experimental colloidal Martensitic transition
Saswati Ganguly*, PS Mohanty, P Schurtenberger, S Sengupta, A Yethiraj
Soft Matter 13 (27), 4689, (2017)
Was selected for cover art of Soft Matter (July 2017)
[14]Crystal to crystal transformation in soft ionic microgels: kinetics and the role of local mechanical susceptibilities
Saswati Ganguly*#, Söfi Nojd, Anand Yethiraj, Peter Schurtenberger, Priti S. Mohanty #